警告
本文最后更新于 2023-10-24,文中内容可能已过时。
tip
学弟去打的,没什么机会去,就复现看看题目难度
确实不难,写这个wp主要是为了把那两个抽象的misc拿出来骂一下
stego
我应该去爱你
最简单的misc
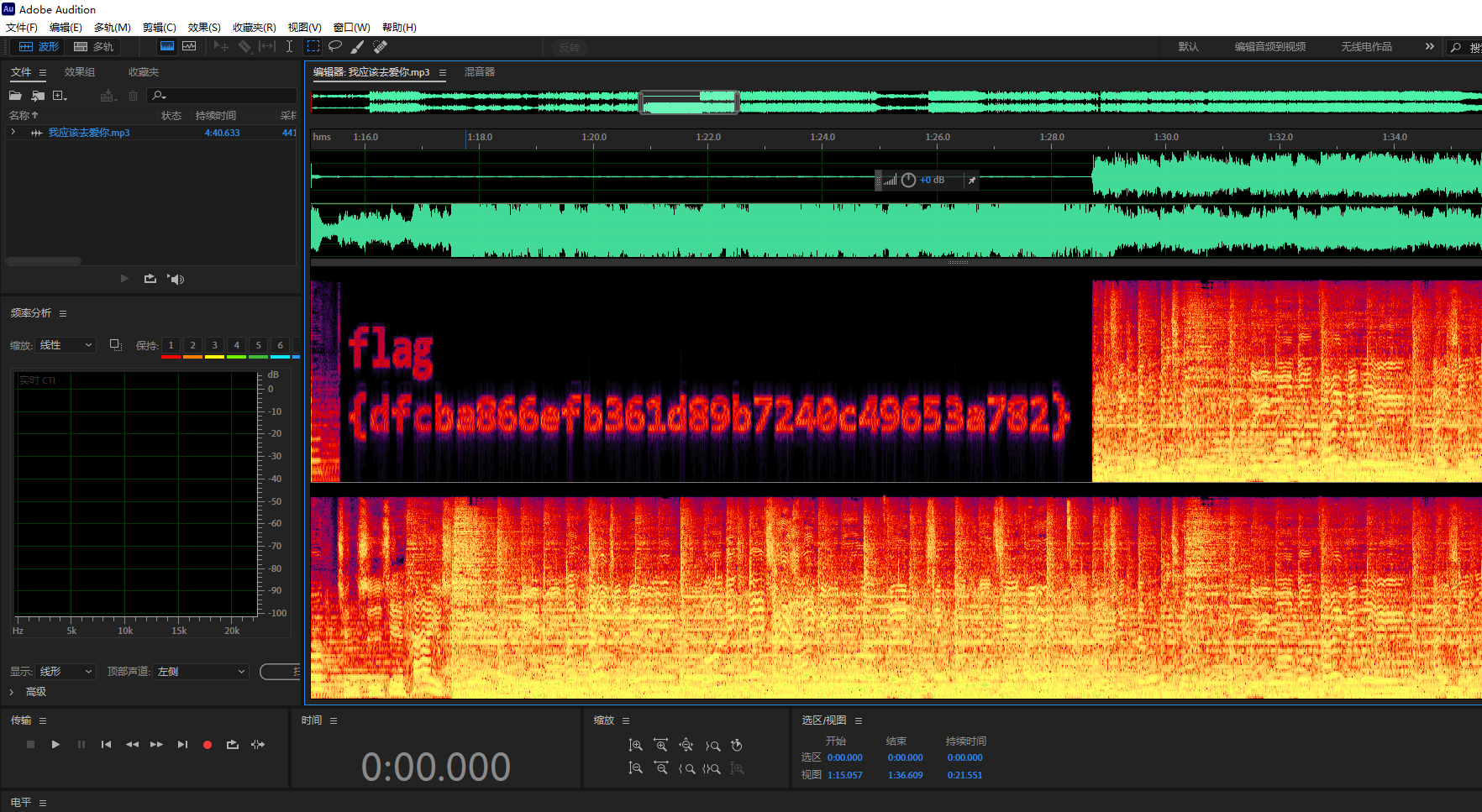
数独
1
|
"".join(["".join([str(x) for x in i]) for i in (sudoku(matrix(ZZ,4,[0,0,0,0,2,0,0,0,0,0,1,0,0,4,0,3])))])
|
sagemath解一下数独
得到的是cloacked-pixel的密码

莫生气
jpg文件尾有个缺了文件头的PNG
补上16字节的文件头
1
|
89 50 4E 47 0D 0A 1A 0A 00 00 00 0D 49 48 44 52
|
python3版本的bwm 双图盲水印
1
|
python3 /root/ctf/BlindWaterMark/bwmforpy3.py decode flag.jpeg 2.png flag.png
|
jpg在前大概会清楚点

misc
复现没有远端环境,看不到签到
简单编码
1
|
0122 110001 0153 0172 1010010 1000101 061 1011010 1010111 1101100 1100100 1001000 0122 0124 1001110 0105 0124 110000 064 1111010 0121 060 0144 1011010 1001101 1101100 1010010 0110 0124 1010110 1110000 1010101 1010010 060 1000110 0141 0126 0105 1101100 0117 1010101 1101100 1100100 1001000 0127 0126 0154 1010101 0124 0125 065 0123 0126 1000101 1100011 060 1001101 110000 0122 0110 0124 1010110 1110000 1010111 1010010 110000 110000 0171 1010110 0105 0144 1001110 1010101 1101100 1100100 1001000 0127 0126 1110000 0125 1010101 1010101 061 0141 1010101 110000 1100100 1001110 1010111 1101011 1010010 1001000 0124 0153 0112 0125 1010010 110000 1101011 0172 0122 0105 110001 0117 1010101 0154 0132 1001000 1010111 0124 1001010 0105 0124 1010101 065 1001011 1010110 1000101 0143 110000 1010111 1101100 1010010 0124 0124 0154 0112 0127 1010010 110000 060 0171 1010010 0105 1100100 0117 0125 1101100 0144 1001000 1010100 0124 0116 1000101 1010010 110000 110101 1010011 1010101 060 0144 1001110 1001110 1000110 0122 1001000 1010100 1101100 1110000 1011001 0124 0126 0105 111001 1010000 1010100 060 071 1010000 1010100 060 111101
|
2 8进制混合
1
|
print("".join(list(map(chr,[int(i,2) if len(i)> 4 else int(i,8) for i in open('0db049060e56b4533427d8ec47624406.txt','r').read().split()]))))
|
神秘的base
EvAzEwo6E9RO4qSAHq42E9KvEv5zHDt34GtdHGJaHD7NHG42bwd=
神奇密码:
xbQTZqjN8ERuwlzVfUIrPkeHd******LK697o2pSsGD+ncgm3CBh/Xy1MF4JAWta
这题很难绷得住,表是反的,非常怀疑是出题人出错了
找到缺的表 然后尝试爆破就行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
import string
import itertools
import base64
raw_table = string.ascii_uppercase+string.ascii_lowercase +string.digits+"+/"
lack_table = "xbQTZqjN8ERuwlzVfUIrPkeHd******LK697o2pSsGD+ncgm3CBh/Xy1MF4JAWta"
lack = "".join([i for i in raw_table if i not in lack_table])
print(lack)
for i in itertools.permutations(lack, len(lack)):
table = "xbQTZqjN8ERuwlzVfUIrPkeHd%sLK697o2pSsGD+ncgm3CBh/Xy1MF4JAWta"% "".join(i)
cipher = "EvAzEwo6E9RO4qSAHq42E9KvEv5zHDt34GtdHGJaHD7NHG42bwd="
flag = base64.b64decode(cipher.translate(str.maketrans(raw_table,table )))
if all(chr(i) in string.ascii_lowercase+string.digits+"{}" for i in flag):
print(flag.decode())
|
crypto
小试牛刀
1
|
print("".join([chr(ord(v)-3-i) for i,v in enumerate("ipfm\x82Kj]p~l?\x82ogw\x85mt[K\x8br\x97")]))
|
被称为"变异凯撒"的题型,不知道谁传出来的名字
easyRSA
先CRT恢复p_2
然后Factoring with High Bits Known(一般叫做p的高位泄露)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# sage
from Crypto.Util.number import *
di = [205329935991133380974880368934928321273, 274334866497850560640212079966358515253, 264739757264805981824344553014559883169, 314495359937742744429284762852853819407, 197513216256198287285250395397676269263, 194633662721082002304170457215979299327, 320085578355926571635267449373645191637, 310701821184698431287158634968374845899, 198238777199475748910296932106553167589, 292201037703513010563101692415826269513, 332238634715339876614712914152080415649, 334257376383174624240445796871873866383]
re = [108968951841202413783269876008807200083, 29053101048844108651205043858001307413, 243503157837867321277650314313173163504, 160933173053376016589301282259056101279, 53063624128824890885455759542416407733, 34980025050049118752362228613379556692, 132553045879744579114934351230906284133, 160998336275894702559853722723725889989, 87211131829406574118795685545402094661, 36445723649693757315689763759472880579, 11133325919940126818459098315213891415, 1404668567372986395904813351317555162]
p4 = CRT(re,di)
print(p4)
print(hex(p4))
n = 23074300182218382842779838577755109134388231150042184365611196591882774842971145020868462509225850035185591216330538437377664511529214453059884932721754946462163672971091954096063580346591058058915705177143170741930264725419790244574761160599364476900422586525460981150535489695841064696962982002670256800489965431894477338710190086446895596651842542202922745215496409772520899845435760416159521297579623368414347408762466625792978844177386450506030983725234361868749543549687052221290158286459657697717436496769811720945731143244062649181615815707417418929020541958587698982776940334577355474770096580775243142909913
e = 0x10001
p4 = p4 >>128
pbits = 1024
kbits = pbits - p4.nbits()
print(p4.nbits())
print(kbits)
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
p = p4+int(roots[0])
print ("p =", p)
print ("q =", n/p)
p= 157397749849472741302651922559110947585741898399548366071672772026799823577871183957882637829089669634665699886533302712057712796808672023827078956556745522749244570015492585747076324258912525658578733402979835176037760966294532155059241756382643278063578661030876735794708282102407491782299777228899079176117
q= 146598666145389487374076474702380241089893944436923994466470555513748278755568038863819188404588602962888679358728628069490879689376996830110571995521814075973422513105805715524894550773219606972944401957227665252279176873209924236114228003156706532596699592716796867748104565680326123749660658940264843181589
c = 16054555662735670936425135698617301522625617352711974775378018085049483927967003651984471094732778961987450487617897728621852600854484345808663403696158512839904349191158022682563472901550087364635161575687912122526167493016086640630984613666435283288866353681947903590213628040144325577647998437848946344633931992937352271399463078785332327186730871953277243410407484552901470691555490488556712819559438892801124838585002715833795502134862884856111394708824371654105577036165303992624642434847390330091288622115829512503199938437184013818346991753782044986977442761410847328002370819763626424000475687615269970113178
n=p*q
phi_n=(p-1)*(q-1)
d=inverse(e,phi_n)
m=pow(c,d,n)
print(m)
print(bytes.fromhex(hex(m)[2:]).decode())
|
pkrsa(未解出)
看起来是PKCS5 v1.5对于padding的攻击
找到几篇文章
http://mslc.ctf.su/wp/google-ctf-spotted-wobbegong-crypto-100/
https://medium.com/asecuritysite-when-bob-met-alice/whats-so-special-about-pkcs-1-v1-5-and-the-attack-that-just-won-t-go-away-51ccf35d65b7
forensic
不太想做,就想写一下最抽象的那题的那步
小刘的硬盘
r-studio挂载,然后能发现几个文件
jpg和txt都没有用
zip里面是flag
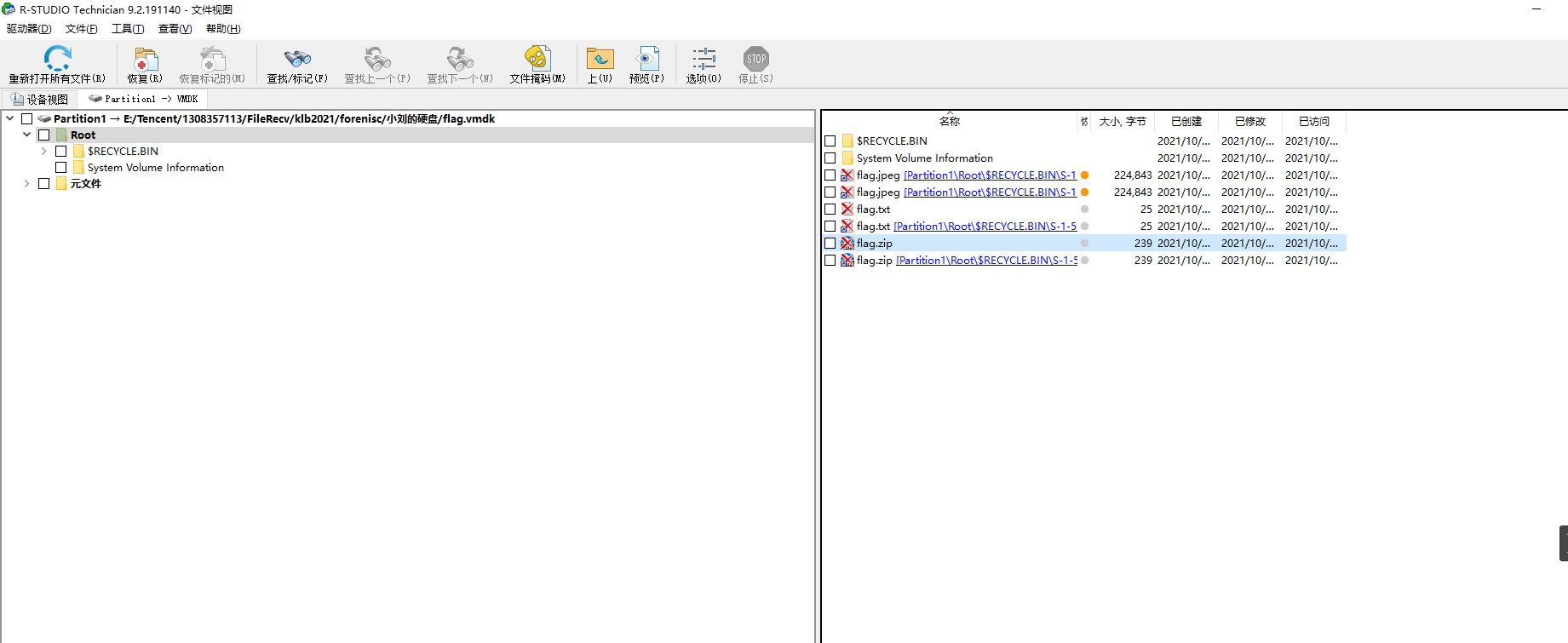
重点是这个压缩包密码
压缩包注释
小刘喜欢用自己的名字+生日当密码
中文密码
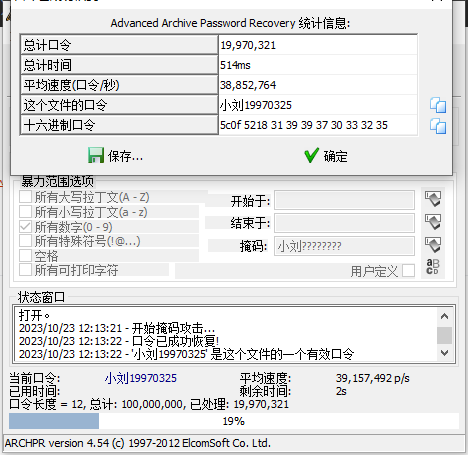
唉 CTF




